
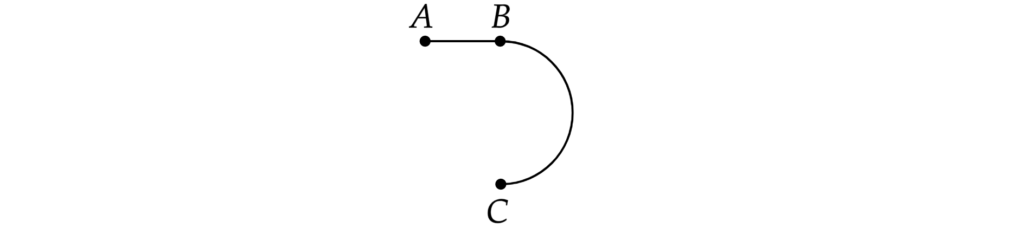
Задание 29. Стартуя из точки А, спортсмен движется равноускоренно до точки В, после которой модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время, затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения на обоих участках одинаков? Траектория ВС — полуокружность.
Решение задачи
Ускорение на прямолинейном участке определяется по формуле:
\( a_{1}=\frac{v}{t_{1}} \)
Где \( v \) — скорость в точке В, а \( t_{1} \) — время движения по прямолинейной траектории.
Ускорение движения по дуге окружности есть центростремительное ускорение и определяется по формуле:
\( a_{2}=\frac{v^2}{R} \)
Где R — радиус полуокружности.
С учётом того, что скорость определяется по формуле \( v=\frac{\pi R}{t_{2}} \), получим \( a_{2}=\frac{v \pi}{t_{2}} \).
Ускорение на обоих участках одинаково, поэтому приравняем \( a_{1} \) и \( a_{2} \):
\( \frac{v}{t_{1}}=\frac{v \pi}{t_{2}} \)
Получим искомое отношение:
\( \frac{t_{1}}{t_{2}}=\pi \)
Ответ к задаче
Ответ: \( \pi \)