
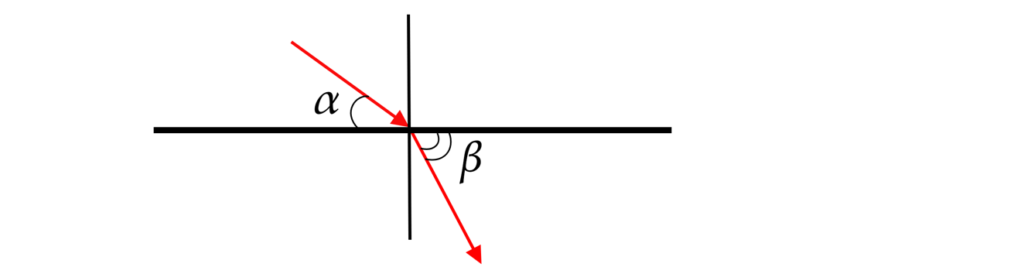
Задание 15. Угол между падающим лучом и границей раздела двух сред равен α=30°, а угол между преломленным лучом и границей раздела двух сред равен β=60°. Найдите относительный показатель преломления второй среды к первой. Ответ округлить до десятых.
Решение задачи
Относительный показатель преломления второй среды к первой найдем из закона преломления:
\( \frac{n_2}{n_1}=\frac{\sin\alpha_1}{\sin\beta_1} \) (1)
Где sinα1 — синус угла падения луча, sinβ1 — синус угла преломления.
Синус угла падения определяется формулой:
\( \sin\alpha_1=\sin(90-\alpha) \) (2)
Синус угла преломления определяется формулой:
\( \sin\beta_1=\sin(90-\beta) \) (3)
Подставим формулы (2) и (3) в формулу (1):
\( \frac{n_2}{n_1}=\frac{\sin(90-\alpha)}{\sin(90-\beta)}=\frac{\sin(90-30)}{\sin(90-60)}=\frac{\sin60}{\sin30} \)
Подставим числовые значения в конечную формулу:
\( \frac{n_2}{n_1}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}≈1,7 \).
Ответ к задаче
Ответ: 1,7.