
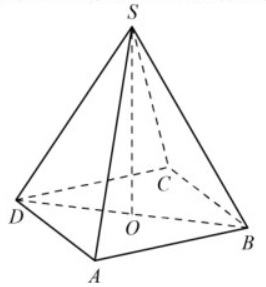
Задание 8. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SD=10, SO=6. Найдите длину отрезка AC.
Решение задачи
В правильной пирамиде вершина проецируется в центр основания. SO является высотой пирамиды. По теореме Пифагора отрезок AC:
\( AC=2AO=2OD=2\sqrt{SD^2-SO^2} \)
Подставим числовые значения в формулу.
\( AC=2\sqrt{10^2-6^2}=2*8=16 \).
Ответ к задаче
Ответ: 16.