
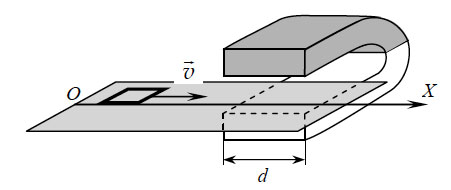
Задание 31. Квадратную рамку из медной проволоки со стороной b = 5 см и сопротивлением R = 0,1 Ом перемещают вдоль оси Ох по гладкой горизонтальной поверхности с постоянной скоростью v. Начальное положение рамки изображено на рисунке. За время движения рамка успевает пройти между полюсами магнита и оказаться в области, где магнитное поле отсутствует. Ширина полюсов магнита d = 20 см, магнитное поле имеет резкую границу и однородно между полюсами, а его индукция B = 1 Тл. Возникающие в рамке индукционные токи нагревают проволоку. Чему равна скорость движения рамки, если за время движения в ней выделяется количество теплоты Q = 2,5·10−3 Дж?
Решение задачи
Запишем формулу ЭДС индукции:
\( |E_{i}|=\frac{|ΔФ|}{|Δt|} \)
При пересечении рамкой границы области поля со скоростью v изменяющийся магнитный поток создаёт ЭДС индукции:
\( |E_{i}|=Bvb \)
Сила тока в это время равна:
\( I=\frac{|E_{i}|}{|R|}=\frac{Bvb}{R} \) (1)
Ток протекает в рамке только во время изменения магнитного потока (при входе в пространство между полюсами и при выходе).
Это время равно:
\( t=\frac{2b}{v} \) (2)
Согласно закону Джоуля-Ленца в проволоке выделится количество теплоты:
\( Q=I^2Rt \) (3)
Подставим формулы (1) и (2) в формулу (3):
\( Q=\frac{2B^2vb^3}{R} \)
Выразим из формулы количества теплоты скорость движения рамки:
\( v=\frac{QR}{2B^2b^3} \)
Подставим числовые значения в формулу.
\( v=\frac{0,0025*0,1}{2*1^2*0,05^3}=1 \) м/с.
Ответ к задаче
Ответ: v = 1 (м/с).